Calculator art: Ordered dithering
I found a way to draw 1-bit sketches in TI-BASIC on my calculator using dithering. I used ordered dithering because it is the easiest to implement, and all that is needed on a 96×64 screen. Below is the code I used, with comments.
First, set a 4×4 Bayer matrix to [J].
:[[1,9,3,11][13,5,15,7][4,12,2,10][16,8,14,6]]/17→JThis will clear drawings, but make sure your graphs are also cleared before running this program.
:ClrDrawIterate through each pixel in range, from the top left to the bottom right .
:For(X,0,94)
:For(Y,0,62)We are graphing , a function of and , with a range of , where represents lightness and represents darkness. Here, I am graphing .
:((X/94)+(Y/62))/2→ZNote that matrix indices start at 1
instead of 0 in TI-BASIC.
If is greater than the value of the Bayer matrix at , the pixel will be displayed in black.
:If Z>[J](remainder(X,3)+1,remainder(Y,3)+1)/17
:Then
:Pxl-On(Y,X)
:End
:End
:End
The program ends here. This is how it came out:
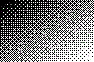
And with more interesting functions, like
remainder(X,Y+1)/(Y+1)→Z:

Or even
(cos(X^2/400)+cos(Y^2/200)+2)/4→Z:

If you try this out, get ready for long drawing times, as TI-BASIC for the Z80 chipset is extremely slow.